8.3. Nevezetes tételek
Néhány korábbi mulasztásunkat pótoljuk.
25. tétel. A háromszög súlyvonalai egy pontban metszik egymást. Ezt a pontot a háromszög súlypontjának nevezzük. A súlypont a súlyvonalakat ![]() arányban osztja, mégpedig úgy, hogy a hosszabb osztási szakasz mindig a csúcs felé esik..
arányban osztja, mégpedig úgy, hogy a hosszabb osztási szakasz mindig a csúcs felé esik..
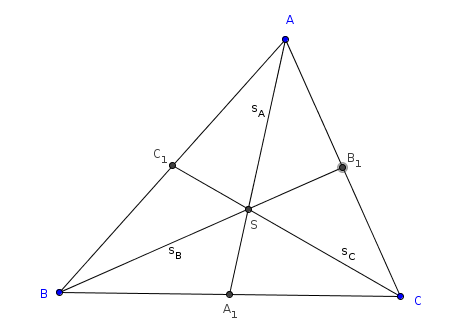
Bizonyítás. Tekintsük 18. ábrát. Húzzuk meg az ![]() és $B$ pontból az
és $B$ pontból az ![]() és
és ![]() súlyvonalakat.
súlyvonalakat.
A két súlyvonal metszéspontja legyen ![]() pont.
pont. ![]() háromszög hasonló
háromszög hasonló ![]() háromszöghöz az alapesetek b) pontja szerint, a hasonlóság aránya
háromszöghöz az alapesetek b) pontja szerint, a hasonlóság aránya ![]() , ezért
, ezért ![]() szakasz párhuzamos
szakasz párhuzamos
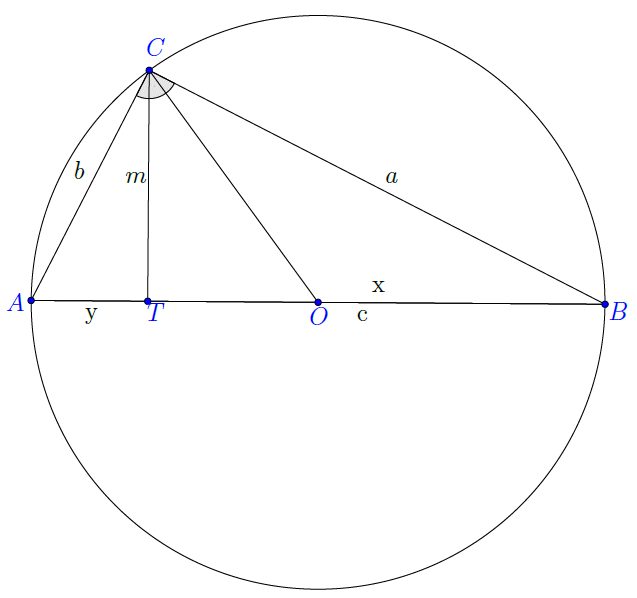
az ![]() oldallal, és fele akkora. Az
oldallal, és fele akkora. Az ![]() hasonló az
hasonló az ![]() -gel, mert szögeik egyenlőek:
-gel, mert szögeik egyenlőek: ![]() (mert csúcsszögek) és
(mert csúcsszögek) és ![]() (mert váltószögek), s így a harmadik szögük is egyenlő. Mivel
(mert váltószögek), s így a harmadik szögük is egyenlő. Mivel ![]() szakasz fele az
szakasz fele az ![]() szakasznak, ezért a
szakasznak, ezért a ![]() és
és ![]() hasonlósági aránya szintén
hasonlósági aránya szintén ![]() . Ebből következik, hogy
. Ebből következik, hogy ![]() és
és ![]() . Az
. Az ![]() metszéspont tehát
metszéspont tehát ![]() arányban osztja a súlyvonalakat, mégpedig úgy, hogy a hosszabb osztási szakasz a csúcs felé esik. A fenti gondolatmenetet
arányban osztja a súlyvonalakat, mégpedig úgy, hogy a hosszabb osztási szakasz a csúcs felé esik. A fenti gondolatmenetet ![]() és
és ![]() súlyvonalakra megismételve kiderül, hogy ezek metszéspontja
súlyvonalakra megismételve kiderül, hogy ezek metszéspontja ![]() -t szintén
-t szintén ![]() arányban osztja, mégpedig úgy, hogy a hosszabb osztási szakasz a csúcs felé esik. Ebből következik, hogy
arányban osztja, mégpedig úgy, hogy a hosszabb osztási szakasz a csúcs felé esik. Ebből következik, hogy ![]() és
és ![]() is épp
is épp ![]() -ben metszi egymást. Az eddigiekből a tétel állításai következnek.
-ben metszi egymást. Az eddigiekből a tétel állításai következnek.![]()
26. tétel (Magasság- és befogótétel). Az ![]() derékszögű háromszögben az átfogóhoz tartozó
derékszögű háromszögben az átfogóhoz tartozó ![]() magasság talppontja legyen
magasság talppontja legyen ![]() ,
, ![]() és
és ![]() .
.
Ekkor ![]() ,
, ![]() és
és ![]() .
.
Bizonyítás. Tekintsük 19. ábrát, az ![]() hegyesszögeit jelölje
hegyesszögeit jelölje ![]() és
és ![]() a szokásoknak megfelelően. Az
a szokásoknak megfelelően. Az ![]() -ben van egy
-ben van egy ![]() szög és egy derékszög, így
szög és egy derékszög, így ![]() , és
, és ![]() . Hasonlóan kapjuk, hogy
. Hasonlóan kapjuk, hogy ![]() , s így természetesen
, s így természetesen ![]() is. A három hasonlóságban a megfelelő oldalak arányának egyenlőségéből kapjuk rendre, hogy
is. A három hasonlóságban a megfelelő oldalak arányának egyenlőségéből kapjuk rendre, hogy ![]() ,
, ![]() és
és ![]() . Ezeket átrendezve a tétel állításai következnek.
. Ezeket átrendezve a tétel állításai következnek. ![]()
A hasonlóságok elemi alkalmazásainak egyik legszebb tétele a következő.
27. tétel (Feuerbach-kör). Egy (hegyesszögű) háromszögben a magasságok talppontjai, az oldalfelező pontok, és a magasságpontot a csúcsokkal összekötő szakaszok felezőpontjai mind illeszkednek egy körre!
Az érdeklődő olvasók a hasonlóságokon alapuló bizonyítást megtalálhatják például itt.