8.5. Oszthatósági szabályok a tízes számrendszerben

I. Az oszthatósági szabályok számok utolsó számjegyei alapján

1. Az utolsó számjegy alapján

a) 10-zel való oszthatóság

A helyi érték táblázat alapján, ha egy szám osztható 10-zel, akkor a 10-nek többszöröse, ezért 0-ra végződik.

Ha egy szám 0-ra végződik, akkor egész számú tízesből áll, tehát osztható 10-zel.

Figyeljük meg az állítások szerkezetét:

Az állítás: Ha egy természetes szám osztható 10-zel, akkor 0-ra végződik.

Az állítás megfordítása: Ha egy természetes szám 0-ra végződik, akkor osztható 10-zel.

Az állítás és a megfordítása egyben:

Egy természetes szám pontosan akkor osztható 10-zel, ha 0-ra végződik.

Az eredeti állítás ekvivalens a következővel:

Ha egy természetes szám nem 0-ra végződik, akkor nem osztható 10-zel.

Az állítást általában ez utóbbi formában használjuk.

(Formálisan az állítás:  , a megfordítása pedig .)

b) 2-vel való oszthatóság

A természetes számot felbontjuk tízesekre és egyesekre: 456 = 450 + 6

A tízesek 10 többszörösei, ezért oszthatók 10-zel, a 10 osztható 2-vel, így a tranzitivitás miatt a tízesek oszthatók 2-vel. Az összeg első tagja osztható 2-vel, ekkor az összeg pontosan akkor osztható 2-vel, ha a második tagja, azaz az egyesek helyén álló számjegy osztható 2-vel.

Egy természetes szám pontosan akkor osztható 2-vel, ha a végződése 0; 2; 4, 6 vagy 8.

A 2-vel osztható számokat nevezzük páros számoknak. A gyerek azt tapasztalják, hogy a szám páros, ha páros számjegyre végződik.

c) 5-tel való oszthatóság

Egy természetes szám pontosan akkor osztható 5-tel, ha 0-ra vagy 5-re végződik.

Ezt a 2-vel való oszthatósághoz hasonlóan mutathatjuk meg.

Az utolsó számjegy alapján a 10 osztóival való oszthatóságot lehet eldönteni.

2. Az utolsó két számjegy alapján

a) 100-zal való oszthatóság

A 10-zel való oszthatósághoz hasonlóan mutatható meg a helyi érték táblázat alapján.

Egy természetes szám pontosan akkor osztható 100-zal, ha két 0-ra végződik.

b) 4-gyel való oszthatóság

Bontsuk fel a számot százasokra, és az utolsó két számjegyből álló számra:

3428 = 3400 + 28.

A százasok oszthatók 100-zal, és így a 100 osztójával, azaz 4-gyel is. Az összeg első tagja osztható 4-gyel, ekkor az összeg pontosan akkor osztható 4-gyel, ha az összeg második tagja osztható 4-gyek, azaz ha az utolsó két számjegyből álló szám osztható 4-gyel.

Egy természetes szám pontosan akkor osztható 4-gyel, ha az utolsó két számjegyből alkotott szám osztható 4-gyel.

Az utolsó két számjegy alapján a 100 osztóival való oszthatóságot lehet eldönteni.

3. Az utolsó három számjegy alapján az 1000-rel, és az 1000 osztóival, például a 8-cal való oszthatóságot lehet eldönteni.

II. Az oszthatósági szabályok számjegyek összege alapján

9-cel való oszthatóság

Írjuk a számot helyi értékes bontásban:

3728 = 3 · 1000 + 7 · 100 + 2 · 2 + 8 = 3 · (999 + 1) + 7 · (99 + 1) + 2 · (9 + 1) + 8 =

= (3 · 999 + 7 · 99 + 2 · 9) + (3 + 7 + 2 + 8)

Az összeg első tagja 9 többszöröse, a második tagja pedig a számjegyek összege, így az összeg pontosan akkor osztható 9-cel, ha a számjegyek összege osztható 9-cel.

Egy természetes szám pontosan akkor osztható 9-cel, ha a számjegyeinek összege osztható 9-cel.

A 9-cel való oszthatóságon alapul az alábbi bűvész trükk:

www.mathematika.hu/viewpage.php?page_id=100&c_start=10

Hasonló a 3-mal oszthatóság szabálya, hiszen a 3 osztója a 9-nek.

Eldobós játék az oszthatósági szabályok felfedezésére:

Sorban mondunk számokat, az kap egy pontot, aki leghamarabb kimondja a mondott szám 4-es osztási maradékát. A számok: 29; 49; 78; 103; 113; 323, …

Figyeljük meg, hogy úgy érdemes játszani, hogy a 4 többszöröseit leválasztjuk a számról:

29 = 28 + 1; 49 = 40 + 8 + 1; 78 = 40 + 36 + 2; 103 = 80 + 20 + 3; 113 = 100 + 12 + 1;

323 = 300 + 20 + 3, …

Hasonló játékkal felfedeztethető a 9-cel oszthatóság szabálya is.

 

III. Összetett oszthatósági szabályok

Írjuk be a halmazábrába a természetes számokat 0-től 30-ig, ha az egyik halmaz a 2-vel, a másik a 3-mal osztható számok halmaza.

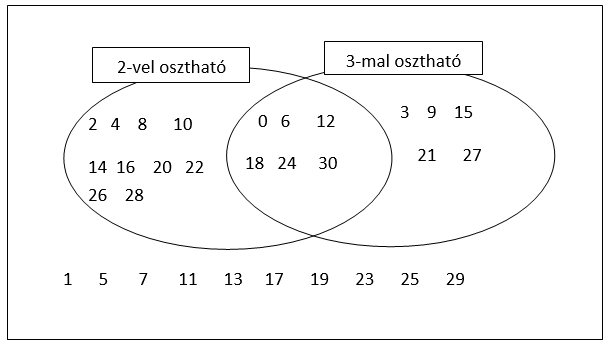
A halmazábra alapján felfedezhető a 6-tal való oszthatóság szabálya:

Egy természetes szám pontosan akkor osztható 6-tal, ha osztható 2-vel és 3-mal.

Példa: Hogyan dönthető el egy természetes számról, hogy osztható-e 24-gyel?

Megoldás: Egy természetes szám pontosan akkor osztható 24-gyel, ha osztható 3-mal és 8-cal, mert a 3 és a 8 relatív prímek.