13.6. Összeadási szabály
1. Útvonalak
Példa: Micimackó otthonából indulva a legrövidebb úton akar eljutni Róbert Gidához úgy, hogy közben három barátját meglátogatja. Játsszuk le az összes lehetséges útvonalat, és rajzoljuk be egy-egy ábrába!
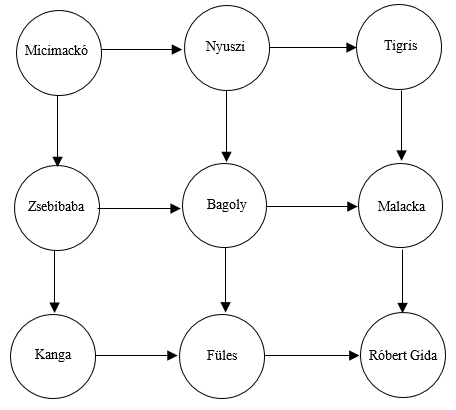
Megoldás:
A példában megfigyelhető az összeadási módszer: Róbert Gidához csak Fülestől vagy Malackától juthat Micimackó. Mivel Micimackó Füleshez és Malackához is 3-féle útvonalon mehet, így Róbert Gidához összesen 3+3=6-féleképpen juthat a lakásától.
Példa:
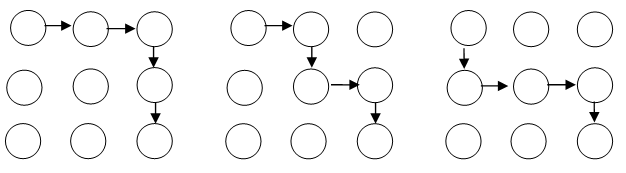
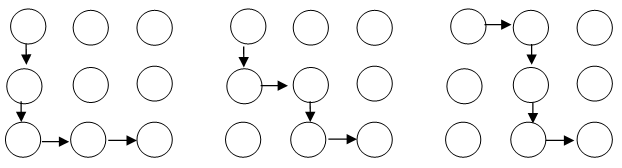
Hányféleképpen lehet kiolvasni a neveket az alábbi betűtáblákból?
|
|
Megoldás:
Írjuk a betűk jobb alsó sarkába azokat a számokat, amik a kezdőpontból a betűbe jutás lehetőségeinek számát mutatják. A ZSUZSI kiolvasásakor a Z-ből a jobbra levő S betűbe 1-féleképpen juthatunk, a lefele levő S betűbe szintén, így 1-et írunk mindkét S betűhöz. A második sorban levő U betűhöz mindkét S-ből juthatunk, így Z-ből U-ba 1+1=2-féleképpen juthatunk, az U-hoz a 2-t írjuk. Így tovább haladva végül az I betűhöz írt számot úgy kapjuk, hogy először megnézzük, hogy honnan juthatunk az I-be: a felső és a balra levő S betűkből. Az I-be juthatunk 4-féleképpen a felső S betűn keresztül, és 6-féleképpen a balra levő S betűből, összesen 4+6=10-féleképpen, azaz a két S betűhöz írt számot összeadjuk.
|
|
Tehát ZSUZSI-t 10-féleképpen lehet kiolvasni, ZSÓFI-t pedig 1+4+6+4+1=16-féleképpen.
A táblázatokban megfigyelhetők a Pascal háromszög számai. A fenti útkereszteződésekben valóban a binomiális együtthatók állnak, hiszen például a ZSUZSI I betűjéhez 5 lépéssel juthatunk, amelyek közül 3 jobbra lépés és 2 lefele lépés. Az út során teljesen mindegy, hogy mikor tesszük meg a jobbra, és mikor a lefele lépéseket, mindenképpen az I-hez jutunk. Így az I-be vezető útvonalak számát megkapjuk, ha összeszámoljuk, hogy hányféleképpen lehet kiválasztani az 5 lépés közül a 3 jobbra lépést (vagy a 2 lefele lépést). Ezek száma: 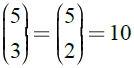 .
.
Példa:
Hányféleképpen lehet eljutni A-ból B-be, ha csak a nyilak mentén haladhatunk?
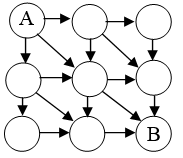
Megoldás:
Írjuk a körökbe azokat a számokat, az előbbi módon, ahányféleképpen A-ból abba a pontba el lehet jutni. Most vannak pontok, ahová három körből is juthatunk, így az azokba írt három számot kell összeadni.
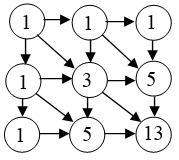
Tehát 13-féleképpen juthatunk A-ból B-be.
2. Esetek szétválasztása
Példa:
Hányféle két vagy háromgombócos fagyit vehetünk, ha a csokoládé, vanília, eper, citrom ízek közül választhatunk, nem veszünk két egyforma ízű gombócot, és a tölcsérben a gombócok sorrendje nem számít?
Megoldás:
Két esetet különböztetünk meg: két- vagy háromgombócos fagyit veszünk.
1. eset: kétgombócos fagyit veszünk.
A négy íz közül választunk kettőt:
A csokihoz választunk háromfélét: csoki-vanília, csoki-eper, csoki-citrom. Csokit többször nem választunk.
A vaníliához már csak kétfélét választhatunk: vanília-eper, vanília-citrom.
Marad az eper-citrom utoljára.
Összesen 3 + 2 + 1 = 6 lehetőség van.
2. eset: háromgombócos fagyit veszünk.
Mivel minden gombóc különböző, négyféle gombóc van, egyet nem választunk közülük. Ezt 4-féleképpen választhatjuk ki.
Tehát a két esetben összesen: 6+4=10 lehetőség van.
A fenti példában összeadtuk a két esetben előforduló lehetőségek számát, ez az összeadási szabály.