A pénz időértéke: jelenérték, jövőérték
A mai pénzösszeg több ok miatt is értékesebb a holnapi ugyanakkora pénzösszegnél:
- a ma rendelkezésre álló pénzösszeg már ma elfogyasztható;
- a ma rendelkezésre álló pénzösszeg befektethető, és a befektetés eredményeként jövedelemre tehetünk szert (például kamatra, osztalékra vagy árfolyamnyereségre).
Ha viszont a pénz nem ugyanannyit ér különböző időpontokban, akkor a különböző időpontokban esedékes pénzösszegeket közvetlenül nem adhatjuk össze, nem vonhatjuk ki egymásból, mint ahogyan a banánt sem adhatjuk össze a naranccsal. Egy pénzösszegről nem elég tudni a nagyságát, a rendelkezésre állásának időpontját is ismernünk kell ahhoz, hogy értékelni tudjuk. Valamilyen módszert, eljárást kell találnunk ahhoz, hogy a különböző időpontokban esedékes pénzösszegeket közös nevezőre hozva dolgozni tudjunk velük. A legkézenfekvőbb megoldás, ha a különböző időpontban esedékes pénzösszegeket egyetlen közös időpontra számítjuk át egy alkalmas kamatláb segítségével. Ennek megfelelően két alapvető módszer is létezik a probléma megoldására, az egyik: a jövőérték-számítás, a másik: a jelenérték-számítás technikája. Minthogy dönteni a jelenben kell, jóval gyakrabban alkalmazzuk a jelenérték-számítást.
A jövőérték-számítás során a különböző időpontokban esedékes pénzösszegeket egy közös, jövőbeli időpontra számoljuk át. A jövőérték tehát megmutatja, hogy a ma befektetett pénzösszeg mekkora összegre gyarapodik egy előre meghatározott időtartam végére egy megfelelő kamatláb alkalmazása mellett. A pénz jövőértékét tulajdonképpen kamatszámítással határozzuk meg.
A jövőérték képlete:
C0(1+r)n , ahol
C0 a jelenbeli pénzösszeg, pl. 100.000 Ft
r: a kamatláb, pl. 10%=0,1
n: az évek (periódusok) száma, pl. 5 év.
(Ekkor a jövőérték 161.051 Ft lesz.)
Tehát bármely adott mai pénzösszeg jövőbeli értékét két tényező határozza meg:
- a kamatláb nagysága, és
- az évek (periódusok) száma.
Egy induló pénzösszeg annál többet ér, minél nagyobb a kamatláb és minél hosszabb ideig kamatozik.
A jelenérték-számítás során arra a kérdésre keressük a választ, hogy valamely a jövőben esedékes pénzösszeg mennyit ér ma. A jelenérték-számítás során a különböző időpontban esedékes pénzösszegeket a mai időpontra számoljuk át. A jelenérték tehát megmutatja egy jövőbeli időpontban esedékes pénzösszeg mai értékét, másként fogalmazva: azt az összeget, amennyit ma kellene befektetni ahhoz, hogy a jövőértéke éppen az az esedékes pénzösszeg legyen. A pénz jelenértékét diszkontálással határozzuk meg. (A gyakorlatban gyakrabban alkalmazzuk a jelenérték-számítást a jövőérték-számításnál, mivel egy döntési szituációban számunkra érdekesebb az, hogy most mennyit ér a döntésük nyomán a jövőben előálló pénzáram. Ezért a későbbiek során a jelenérték-számítás módszerére támaszkodunk majd.)
A jelenérték képlete:
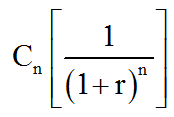 , ahol
, ahol
Cn az n év (periódus) múlva esedékes pénzösszeg, pl. 161.051 Ft
r: a kamatláb, pl. 10%=0,1
n: az évek (periódusok) száma, pl. 5 év
(Ekkor a jelenérték 100.000 Ft lesz.)
A jelenérték-számítás segítségével most már közös nevezőre tudjuk hozni a különböző időpontokban esedékes pénzáramlás-sorozatokat (cash-flow-kat), így ezek - a jelenértékükön - összeadhatóvá, kivonható, összehasonlíthatóvá válnak.